Ik ben van plan een snelle plank te bouwen (zwever).
Dit was een mooi excuus om eindelijk eens XFLR5 te downloaden en ermee te gaan spelen (XFLR5 is een gratis programma waarmee modelvliegtuigen aerodynamisch kunnen worden geanalyseerd).
Qua profiel is de keuze op PW51 gevallen, van Peter Wick.
Beperkingen zoals 'vleugel uit één stuk' en 'moet in de auto passen' beperken de spanwijdte tot een meter of 2.
Eigenlijk ontwerp ik hem voor de helling bij flinke wind, maar in de praktijk zal dat maar één of 2x per jaar voorkomen. Om op het vlakke toch te kunnen vliegen, en niet de lier uit te hoeven zetten, wil ik hem met een elastiek (max 30kg) redelijk hoog kunnen schieten.
Het gewicht moet dan toch wel onder de 3kg blijven (3kg krijg je nog ca. 100m hoog met 30kg startkracht en een meter of 15 rubber).
Gewenst vlieggedrag: 'moet ver en snel kunnen vliegen, vlot rollen en strak de hoek om gaan'. Hoge vleugelbelasting dus.
Dus, welke spanwijdte, slankheid (AR) en vleugelbelasting te kiezen?
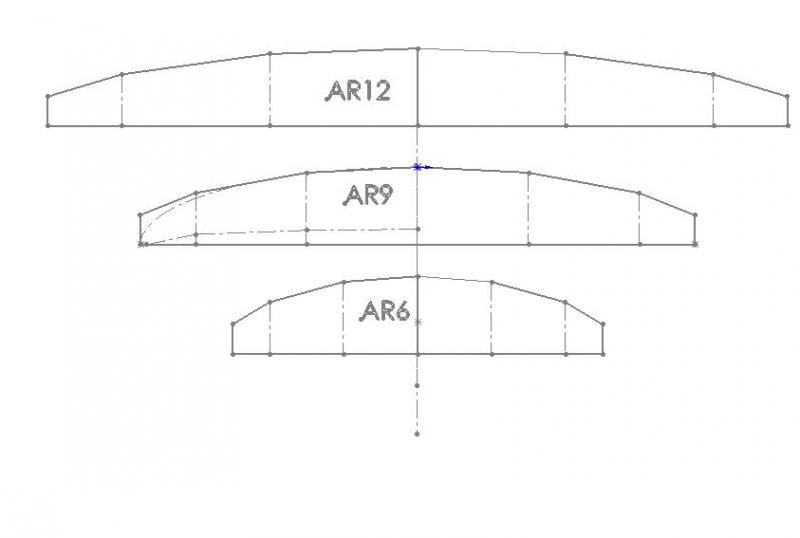
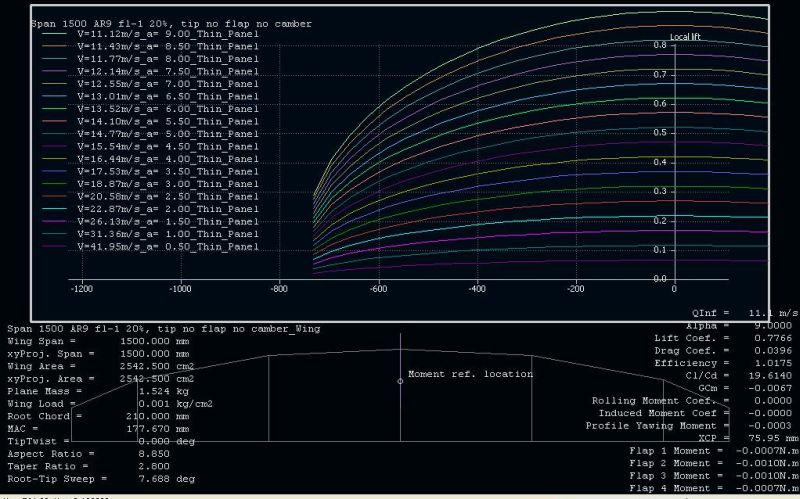
Hieronder een bovenaanzicht van de vleugel, opgebouwd uit 6 panelen.
Contour is vrijwel elliptisch, met iets meer oppervlak in de tips.
Onder elkaar staan slankheid 12, 9 en 6.
Vanuit de theorie geeft een hoge slankheid in principe minder geinduceerde weerstand, wat vooral de glijhoek bij lagere snelheden ten goede komt.
Nadeel is een lager Re-getal (koorde kleiner), minder ruimte voor de servo's (koorde kleiner dus vleugel dunner) en meer 'negative yaw' (ik ken hier geen Nederlands woord voor, ik bedoel de neiging om naar links te draaien als je naar rechts wilt rollen). Vooral omdat het een plank is (dus korte romp) en 'hij geen richtingsroer krijgt, zal dit vervelende effect een rol spelen.
In XFLR heb ik de vleugel gemodelleerd en de flaps ca. 1 graad 'up' getrimd om een nèt stabiel vliegende vleugel te krijgen (géén stabilo).
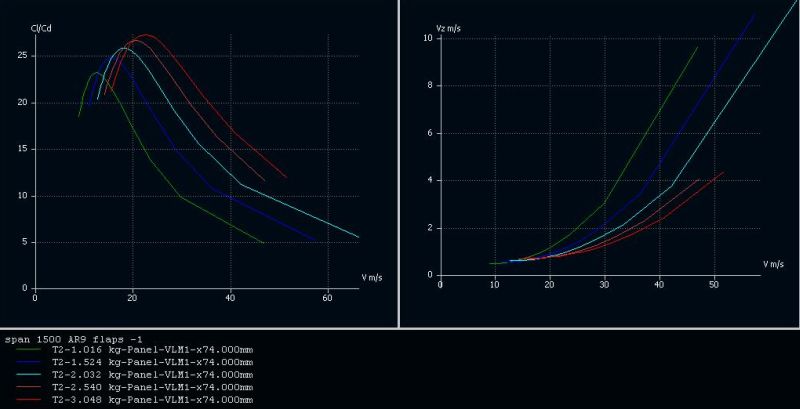
Onderstaand de glijhoek versus de vliegsnelheid voor de 3 slankheden (AR6, 9 en 12) en vleugelbelastingen van 40 tot 120 gram/dm^2.
De slankheden zijn gevarieerd door de spanwijdte aan te passen. Dus alle vleugels hadden een wortelrib van 210mm en een span van 2000, 1500 en 1000mm.
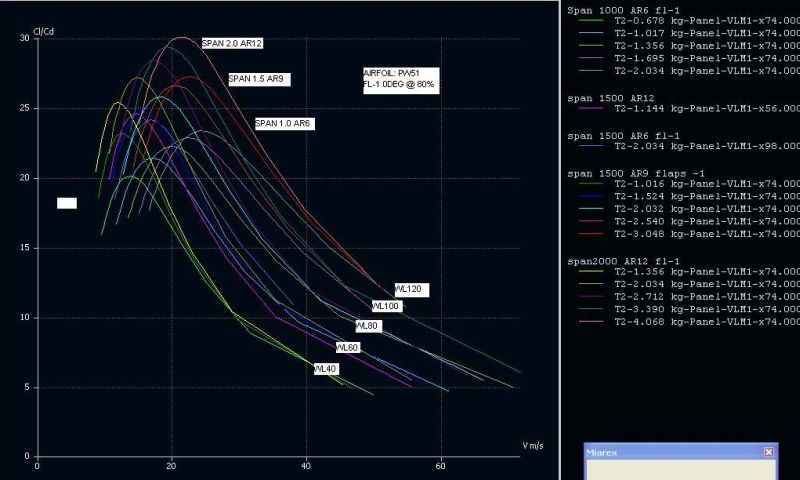
Wat direct opvalt is het effect van slankheid en vleugelbelasting:
- De drie slankheden zijn te herkennen als drie groepjes polaires, schuin onder elkaar.
Hogere slankheid lijkt alleen maar voordelen te hebben: beter glijhoek bij alle snelheden (vooral de lage) en alle vleugelbelastingen...mits de koorde voldoende groot blijft.
De paarse kromme van "span1500 AR12" is slechter dan de "span 1500 AR9" bij gelijke vleugelbelasting (blauwe lijn). Kennelijk wordt het voordeel van de hogere AR teniet gedaan door het kleinere Re-getal.
- Bij elke slankheid geeft een hogere vleugelbelasting een beter glijhoek, behalve bij héél lage snelheden. Dit had ik niet verwacht omdat ik dacht dat de theorie, in elk geval wat betreft profielen (dus oneindig lange vleugels), zegt dat de maximale glijhoek bij een hogere vleugelbelasting gelijk blijft, alleen dat dit maximum bij een hogere snelheid wordt bereikt.
Deze grafiek laat echter zien dat het maximum óók sterk verbeterd bij een hogere belasting.
Misschien komt dit door het hogere Re-getal, maar als iemand een beter verklaring heeft hoor ik het graag.
- Bij echt hoge snelheden (>40m/s) maakt het niet meer uit hoe slank de vleugel is, het gaat alleen nog maar om vleugelbelasting, hoe meer hoe beter.
Voorlopig mik ik op een spanwijdte van 1,5m en een slankheid van 9.
Vleugelbelasting van 40-120gram/dm2 betekent dan een startgewicht van 1100 tot 3000gram.
Dit was een mooi excuus om eindelijk eens XFLR5 te downloaden en ermee te gaan spelen (XFLR5 is een gratis programma waarmee modelvliegtuigen aerodynamisch kunnen worden geanalyseerd).
Qua profiel is de keuze op PW51 gevallen, van Peter Wick.
Beperkingen zoals 'vleugel uit één stuk' en 'moet in de auto passen' beperken de spanwijdte tot een meter of 2.
Eigenlijk ontwerp ik hem voor de helling bij flinke wind, maar in de praktijk zal dat maar één of 2x per jaar voorkomen. Om op het vlakke toch te kunnen vliegen, en niet de lier uit te hoeven zetten, wil ik hem met een elastiek (max 30kg) redelijk hoog kunnen schieten.
Het gewicht moet dan toch wel onder de 3kg blijven (3kg krijg je nog ca. 100m hoog met 30kg startkracht en een meter of 15 rubber).
Gewenst vlieggedrag: 'moet ver en snel kunnen vliegen, vlot rollen en strak de hoek om gaan'. Hoge vleugelbelasting dus.
Dus, welke spanwijdte, slankheid (AR) en vleugelbelasting te kiezen?
Hieronder een bovenaanzicht van de vleugel, opgebouwd uit 6 panelen.
Contour is vrijwel elliptisch, met iets meer oppervlak in de tips.
Onder elkaar staan slankheid 12, 9 en 6.

Vanuit de theorie geeft een hoge slankheid in principe minder geinduceerde weerstand, wat vooral de glijhoek bij lagere snelheden ten goede komt.
Nadeel is een lager Re-getal (koorde kleiner), minder ruimte voor de servo's (koorde kleiner dus vleugel dunner) en meer 'negative yaw' (ik ken hier geen Nederlands woord voor, ik bedoel de neiging om naar links te draaien als je naar rechts wilt rollen). Vooral omdat het een plank is (dus korte romp) en 'hij geen richtingsroer krijgt, zal dit vervelende effect een rol spelen.
In XFLR heb ik de vleugel gemodelleerd en de flaps ca. 1 graad 'up' getrimd om een nèt stabiel vliegende vleugel te krijgen (géén stabilo).
Onderstaand de glijhoek versus de vliegsnelheid voor de 3 slankheden (AR6, 9 en 12) en vleugelbelastingen van 40 tot 120 gram/dm^2.
De slankheden zijn gevarieerd door de spanwijdte aan te passen. Dus alle vleugels hadden een wortelrib van 210mm en een span van 2000, 1500 en 1000mm.

Wat direct opvalt is het effect van slankheid en vleugelbelasting:
- De drie slankheden zijn te herkennen als drie groepjes polaires, schuin onder elkaar.
Hogere slankheid lijkt alleen maar voordelen te hebben: beter glijhoek bij alle snelheden (vooral de lage) en alle vleugelbelastingen...mits de koorde voldoende groot blijft.
De paarse kromme van "span1500 AR12" is slechter dan de "span 1500 AR9" bij gelijke vleugelbelasting (blauwe lijn). Kennelijk wordt het voordeel van de hogere AR teniet gedaan door het kleinere Re-getal.
- Bij elke slankheid geeft een hogere vleugelbelasting een beter glijhoek, behalve bij héél lage snelheden. Dit had ik niet verwacht omdat ik dacht dat de theorie, in elk geval wat betreft profielen (dus oneindig lange vleugels), zegt dat de maximale glijhoek bij een hogere vleugelbelasting gelijk blijft, alleen dat dit maximum bij een hogere snelheid wordt bereikt.
Deze grafiek laat echter zien dat het maximum óók sterk verbeterd bij een hogere belasting.
Misschien komt dit door het hogere Re-getal, maar als iemand een beter verklaring heeft hoor ik het graag.
- Bij echt hoge snelheden (>40m/s) maakt het niet meer uit hoe slank de vleugel is, het gaat alleen nog maar om vleugelbelasting, hoe meer hoe beter.
Voorlopig mik ik op een spanwijdte van 1,5m en een slankheid van 9.
Vleugelbelasting van 40-120gram/dm2 betekent dan een startgewicht van 1100 tot 3000gram.
Laatst bewerkt door een moderator:
 [/EDIT]
[/EDIT]