Bouw Ka-7 schaalzwever 1:4 (4 meter)

[Fotor]

Ik heb wat verder gestoeid met XFLR5.
Allereerst maak je een vliegtuigmodel. De romp kan je ook modelleren, maar dat heb ik achterwege gelaten. Alleen de vleugel en de staartvlakken zijn gemaakt in het model.

Na wat berekeningen volgen er chaotische plaatjes met heel veel pijlen waarvan de functie niet overal duidelijk is. Maar even vergeten dus.

Zo'n vliegtuigmodel is redelijk snel te maken als je wat basic maten hebt van het vliegtuig.
Je kan dit model laten doorrekenen met constante snelheid, maar ook met constante lift, wat veel interessanter is. Als je het gewicht van het vliegtuig opgeeft berekent het programma zelf de combinaties van invalshoek en snelheid om de gewenste lift te krijgen. Bij toenemende invalshoek neemt de snelheid af, en dus ook het Reynolds getal. Wordt allemaal meegenomen in de berekeningen.

Eerst ga je op zoek naar het neutraalpunt. Je gaat met het zwaartepunt schuiven tot de berekeningen een horizontale lijn voor het moment laten zien. Bij dit zwaartepunt zal het vliegtuig niet willen duiken om klimmen als de snelheid verandert. Het neutraal punt kwam uit op 65 mm achter de vleugelneus in het midden van de vleugel (is mijn nulpunt voor het vliegtuigmodel).
Het gewenste zwaartepunt ligt 10% voor het neutraalpunt, de static margin is dus 10%. Dit geeft een gematigde stabiliteit om de dwarsas. Die 10% is een precentage van de 'mean aerodynamic chord', de gemiddelde aerodynamische koorde. Ik het de gemiddelde geometrische koorde genomen, die is 270 mm. Het zwaartepunt met 10% SM komt uit op 65-27 = 38 mm.

Nu ga je het instelhoekverschil aanpassen. Je wilt dat het moment op het vliegtuig 0 is op de ontwerp-CL. De gewenste CL van 0,8 treedt op bij een invalshoek van 6 graden. Bij een instelhoekverschil van 2,5 graad blijkt het moment 0 te zijn bij 6 graden invalshoek.

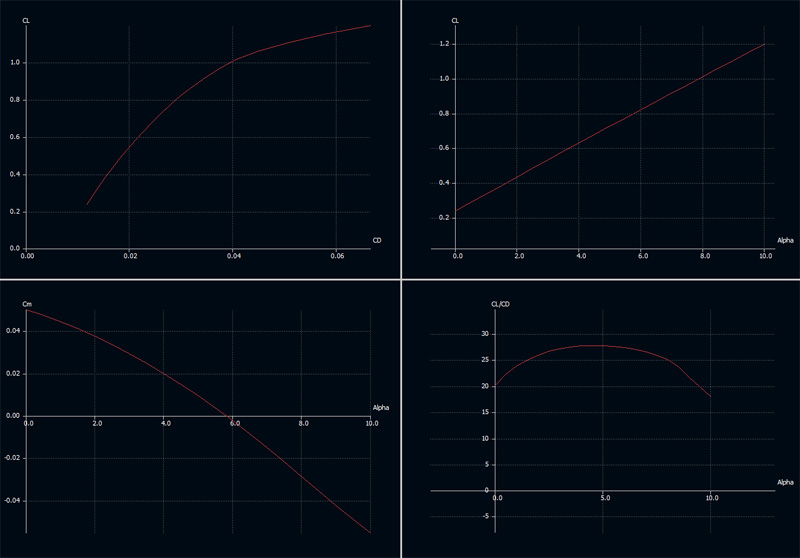
Als ik CL/CD (lees: glijhoek) uitzet tegen invalshoek ligt het optimum bij een krappe 5 graden. Voor de power factor (lees: minimum dalen) ligt het optimum bij een ruime 7 graden. Mijn uitgetrimde situatie bij 6 graden invalshoek ligt hier precies tussenin. Perfect! Het is een gelukkige (goed gegokte....) keuze geweest.

Probleem 1: een instelhoekverschil van 2,5 graad klinkt mij als redelijk veel in de oren. Anderzijds is het vleugelprofiel wel behoorlijk gewelfd (3%) en zit er een behoorlijke tipverdraaiing in de vleugel (het instelhoekverschil tov de tip is 0!). Het zou dus toch wel aardig kunnen kloppen.
Probleem 2: het zwaartepunt (bij 10% SM) wat ik vind ligt behoorlijk achter het opgegeven zwaartepunt. Het zwaartepunt op de tekening ligt op de vleugelneus ter plaatse van de vleugelwortel. Dat scheelt zo'n 40 mm met mijn berekening! Het opgegeven zwaartepunt zou een statische marge inhouden van 24%, dat is wel heel veel.
Er zijn meerdere onzekerheden in de hele berekening. Ik weet niet of er profielverloop is toegepast, de washout is niet exact bekend, de voorwaartse pijlstelling heb ik niet heel exact kunnen meten (een beetje meer voorwaartse pijlstelling betekent een meer voorlijk zwaartepunt), wat voor statische marge heeft de ontwerper aangehouden . Aangezien bij de meeste modellen een voorzichtig (voorlijk) zwaartepunt wordt opgegeven kan ik waarschijnlijk meteen wel een cm naar achteren. Daarna wordt het gewoon proberen wat het model met vliegen doet.

Was deze hele exercitie nuttig? Mwah, voor de bouw misschien niet direct. Maar het was wel een goed excuus om eens gericht met XFLR5 aan de slag te gaan en dat programma wat te leren kennen. Het is minder moeilijk dan ik dacht, maar je moet de werkvolgorde even uitvinden. En ik vind dit leuk om te doen. Dus ja, toch wel een beetje nuttig.

 

[DirkSchipper]

Eerst ga je op zoek naar het neutraalpunt. Je gaat met het zwaartepunt schuiven tot de berekeningen een horizontale lijn voor het moment laten zien. Bij dit zwaartepunt zal het vliegtuig niet willen duiken om klimmen als de snelheid verandert.

Niet helemaal waar (of: anders gezegd ...).
Bij het ZW-punt op het neutraal-punt is het vliegtuig voor alle alfa's indifferent. Er treedt geen moment verandering op agv. een wijziging van instelhoek.

Het neutraal punt kwam uit op 65 mm achter de vleugelneus in het midden van de vleugel (is mijn nulpunt voor het vliegtuigmodel).
Het gewenste zwaartepunt ligt 10% voor het neutraalpunt, de static margin is dus 10%. Dit geeft een gematigde stabiliteit om de dwarsas.

10% static margin (NL:stabiliteitsmarge, DE:stabilitätsmaß) is een waarde voor de geoefende modelpiloot. Beginners zitten eerder op 15% à 20% (de laatste is erg veel).

Die 10% is een precentage van de 'mean aerodynamic chord', de gemiddelde aerodynamische koorde. Ik het de gemiddelde geometrische koorde genomen, die is 270 mm. Het zwaartepunt met 10% SM komt uit op 65-27 = 38 mm.

Yep, maar XFLR5 bereken de MAC voor je. In de plane-view staat hij links onder.

Nu ga je het instelhoekverschil aanpassen. Je wilt dat het moment op het vliegtuig 0 is op de ontwerp-CL. De gewenste CL van 0,8 treedt op bij een invalshoek van 6 graden. Bij een instelhoekverschil van 2,5 graad blijkt het moment 0 te zijn bij 6 graden invalshoek.

Als ik CL/CD (lees: glijhoek) uitzet tegen invalshoek ligt het optimum bij een krappe 5 graden. Voor de power factor (lees: minimum dalen) ligt het optimum bij een ruime 7 graden. Mijn uitgetrimde situatie bij 6 graden invalshoek ligt hier precies tussenin. Perfect! Het is een gelukkige (goed gegokte....) keuze geweest.

Handiger methode:
Maak een grafiek met op de Y-as: Cm en op de X-as: Cl.
Hoe?
Klik met de verkeerde muisknop op de grafiek, en kies "Current graph / Define graph settings ...", etc.

Persoonlijk kies ik de Cl waarbij Cm=0 optreedt altijd tussen minimaal dalen en maximale glijhoek (Cl/Cd-max. resp. Vz-min.)

Probleem 1: een instelhoekverschil van 2,5 graad klinkt mij als redelijk veel in de oren. Anderzijds is het vleugelprofiel wel behoorlijk gewelfd (3%) en zit er een behoorlijke tipverdraaiing in de vleugel (het instelhoekverschil tov de tip is 0!). Het zou dus toch wel aardig kunnen kloppen.

2,5 graden instelhoek verschil is niet veel als je de gekozen Cl eraan koppelt. Normaliter wordt een modelkist gevlogen bij een Cl van 0,6 (metingen van Matthieu Scherrer, zowel op de helling als op het vlakke land). Zo'n Cl levert icm. een statis margin van 10% een duikproef die lekker geleidelijk herstelt. Jij hebt een ontwerp-Cl van 0,8 gekozen. Dat is een waarde waarmee normaliter ge-thermiekt wordt.

Probleem 2: het zwaartepunt (bij 10% SM) wat ik vind ligt behoorlijk achter het opgegeven zwaartepunt. Het zwaartepunt op de tekening ligt op de vleugelneus ter plaatse van de vleugelwortel. Dat scheelt zo'n 40 mm met mijn berekening! Het opgegeven zwaartepunt zou een statische marge inhouden van 24%, dat is wel heel veel.

Ik heb nog nooit een kist gezien met een correct ZW-punt op de tekening (of elders). Altijd veel te ver naar voren. Alpina: opgegeven 80-95mm, Ik vlieg nu met 110mm. Möwe: ik vlieg nu zo'n 40-50mm meer naar achteren.
Neem de waarde uit XFLR5 en ga hooguit 5 mm naar voren als je niet durft.

Er zijn meerdere onzekerheden in de hele berekening. Ik weet niet of er profielverloop is toegepast, de washout is niet exact bekend, de voorwaartse pijlstelling heb ik niet heel exact kunnen meten (een beetje meer voorwaartse pijlstelling betekent een meer voorlijk zwaartepunt), wat voor statische marge heeft de ontwerper aangehouden . Aangezien bij de meeste modellen een voorzichtig (voorlijk) zwaartepunt wordt opgegeven kan ik waarschijnlijk meteen wel een cm naar achteren. Daarna wordt het gewoon proberen wat het model met vliegen doet.

Profielverloop heeft geen invloed op N-punt, dus ook niet op ZW-puntsligging. N-punt is alleeen alhankelijk van het bovenaanzicht van het hele vliegtuig. Raar maar waar, ik geloofde het voorheen ook niet.

Was deze hele exercitie nuttig? Mwah, voor de bouw misschien niet direct. Maar het was wel een goed excuus om eens gericht met XFLR5 aan de slag te gaan en dat programma wat te leren kennen. Het is minder moeilijk dan ik dacht, maar je moet de werkvolgorde even uitvinden. En ik vind dit leuk om te doen. Dus ja, toch wel een beetje nuttig.

Mooi zo! ;-)

Dirk.

 

[Fotor]

Niet helemaal waar (of: anders gezegd ...).
Bij het ZW-punt op het neutraal-punt is het vliegtuig voor alle alfa's indifferent. Er treedt geen moment verandering op agv. een wijziging van instelhoek.

Dat moet invalshoek zijn ipv instelhoek.
Ik interpreteer een snelheidsverandering ook meteen als invalshoekverandering. Als je je vliegtuig naar een andere snelheid brengt en je laat de knuppel los zal hij geen neiging hebben terug te keren naar de oude snelheid (=oude invalshoek) als het zwaartepunt op het neutraalpunt ligt.

Profielverloop heeft geen invloed op N-punt, dus ook niet op ZW-puntsligging. N-punt is alleeen alhankelijk van het bovenaanzicht van het hele vliegtuig. Raar maar waar, ik geloofde het voorheen ook niet.

Dirk, voor deze voorwaarts gepijlde vleugel lijkt het me wel invloed hebben. Stel dat je de washout minder maakt (of bijv de welving bij de tip groter), dan gaat de lokale Cl bij de tippen omhoog. Als de tippen relatief meer lift gaan leveren gaat het neutraalpunt van de hele vleugel naar voren. Toch??
Dank voor je andere inputs.

 

[Fotor]

Denkfout: bij minder washout gaat drukpunt naar voren, maar mogelijk verandert ook de heling van de Cm lijn. Misschien heb je toch gelijk. Ik ga hier op weg naar madeira eens over nadenken. Vanavond wat proberen met XFLR5.

 

[DirkSchipper]

Als de tippen relatief meer lift gaan leveren gaat het neutraalpunt van de hele vleugel naar voren. Toch??

Denkfout: bij minder washout gaat drukpunt naar voren, maar mogelijk verandert ook de heling van de Cm lijn. Misschien heb je toch gelijk. Ik ga hier op weg naar madeira eens over nadenken. Vanavond wat proberen met XFLR5.

Onderweg zou ik (als ik jou was) aan wat anders denken. Voor je het weet zit je in Kaapstad, tegen een berg, op de zeebodem ...

Ik kan je twijfels helemaal volgen. Ook ik heb dit nooit kunnen verklaren, maar allerlei (in mijn ogen) Model-aerodynamica-kenners zeggen hetzelfde. Bovendien, als je in een aerodynamisch reken programma de layout van een kist invoert berekent hij het N-punt. Ongeacht het profiel.

Ik ben benieuwd of jij een verklaring vindt die steekhoudt. Het verhaal met veranderend drukpunt komt gevoelsmatig correct over, maar kennelijk denken de 'echt groten' daar anders over.

Dirk

Edit:
Een beetje gezocht op "calculate neutral point".
Twee rekenvoorbeelden gevonden (A en B).
Beide lijken me consistent tov. elkaar.
Factoren die een rol spelen zijn vleugel- en stabilo-oppervlakte, lengte staartboom, de Cl-verandering per instelhoekverandering (dCl/dα)voor vleugel en stabilo-profielen.
Washin/-out maakt dus niets uit, mits je binnen vliegbare instelhoeken blijft (maar dan geldt dCl/dα niet meer).

 

[Fotor]

Net even wat gespeeld met XFLR5, en de vorm van de Cm-alpha grafiek blijft inderdaad min of meer gelijk bij het aanpassen van de washout. Onderweg heb ik geen sluitende verklaring kunnen vinden, maar het zal wel kloppen zo. Gevoelsmatig komt het vreemd op me over dat als je op een gepijlde vleugel de washout aanpast, dat dan het neutraalpunt (en dus ook het gewenste zwaartepunt) niet verloopt.
Weer wat geleerd (en weer heel thuis ).

 

[Fotor]

Op de achtergrond wordt nog wat gerekend, maar nu eerst weer eens wat bouwfoto's.

Het skelet van het hoogteroer is opgebouwd. De scharnieren worden alvast in het stabilo gelijmd. De scharnieren worden zo ver mogelijk in het hoogteroer getrokken, de stokjes allemaal even recht naar beneden laten wijzen voor het uitlijnen. Dan de boel met lijm in het stabilo schuiven en zorgen dat de voorlijst van het hoogteroer mooi recht is. Als die voorlijst niet mooi recht gehouden zou worden komen de scharnierpunten van de scharnieren niet in één lijn te liggen. Het lijmen van de scharnieren in het hoogteroer gebeurt pas na het bespannen.
De lijm smeer ik in de gaten waar de scharnieren in komen, niet op de scharnieren zelf. Zo loopt het teveel aan lijm verder het gat in als je het scharnier erin schuift. Als je de lijm op het scharnier aanbrengt loopt het teveel aan lijm terug langs je scharnier, en met een beetje pech gaat het in het scharnierpunt zitten. Als alles op zijn plek zit breng ik alsnog een heel klein beetje epoxy aan op het scheidingsvlak van stabilo-achterlijst en scharnier.
De scharnieren werken goed, het roer loopt soepel op en neer.

Voor het maken van het trimvlak wordt een deel van de ribben en achterlijst nu weggesneden.

Daar komt een nieuw achterlijstje. Wat verstevigingsdriehoekjes erin voor de stijfheid. Het trimvlak zelf is gesneden uit een balsa achterlijstprofiel.

Voor de sleephaak heb ik in de zijkant van de romp een strook triplex ingelijmd. Daarachter is de sleephaak gelijmd met epoxy. Het spant waar de sleephaak tegenaan zit is hetzelfde spant waar de cockpit voor eindigt. De sleephaak zit dus onder de voorste begrenzing van de kap.

In de wortelribben (zowel de romp- als de vleugelzijde) heb ik uitsparingen gemaakt voor de stekkerverbinding voor de rolroeren en remkleppen. Deze uitsparingen zijn gemaakt met een frees-opzetstuk voor mijn dremel.

De wortelribben voor de romp zijn op hun plaats gelijmd met epoxy. Ze hebben niet alleen houvast aan de 2 spanten, maar ook aan de gording waar ze mooi vlak tegen liggen.

 

[Fotor]

Meningen graag

Tijdens het klussen zat ik naar het kielvlak te kijken, en ik kreeg ineens een brainfart. Zou ik het kielvlak niet makkelijk verwijderbaar kunnen maken? Het zou het transport en de montage van het stabilo/hoogteroer makkelijker maken. Het richtingroer wordt sowieso demontabel.

Het idee: tussen de 2 rompgordingen (die lange latten die naar voren lopen, waar alle spanten tussen zitten) komt zowel links als rechts een plaatje stevig multiplex. Aan de ene kant een verzonken gat in het multiplex, op het tegenover gelegen plankje een moer aan de binnenkant op het multiplex gelijmd. Op het plaatje dat uit het kielvlak steekt ook een moer gelijmd. De 2 moeren en het verzonken gat zijn natuurlijk met elkaar uitgelijnd. Kielvlak in de romp steken, bout erdoor en het kielvlak zit vast. Kielvlak kan niet voor- en achteruit, niet naar links of recht (door die moer op het kielvlak zelf) en het kan niet naar boven.

Vraag: zou dit sterk genoeg zijn? Er komt een flink richtingroer achter te hangen.
Mijn idee: ik probeer het gewoon en kijk hoe sterk het aan gaat voelen. Vastlijmen kan altijd nog. Maar misschien zeggen jullie: niet aan beginnen.

 

[Ariel]

Demontabel kielvlak is zeker handig gezien de afmetingen.
Je wil links en rechts stevig multiplex gebruiken voor de schroef om het kielvlak vast te zetten. Dat is prima.
Het zwakke punt is het populieren(?) triplex wat uit het kielvlak steekt.
Dit zou ik versterken voor de zekerheid.
Niet dat het meteen stuk gaat maar naar een aantal klappen kan het spontaan breken.

Johannes

 

[Fotor]

Tja, dat had ik dan eigenlijk tijdens de bouw van het kielvlak moeten vervangen door goed triplex (maar ja, achteraf kijk je een koe in zijn ....). Ik zie niet hoe ik dat nu goed kan versterken zonder een zwak punt bij de wortel van het kielvlak te houden. Je hebt wel een punt Johannes.

 

[bdoets]

Toch kan ik me eigenlijk niet voorstellen dat de zijdelingse krachten die de lucht op richtingsroer en kielvlak uitoefent, sterker kunnen zijn dan dat stuk hout.
Stel dat je een boot had, en hiermee het (water)roer vast zat. Tja, dan zou het misschien krap worden.
In de oorspronkelijke constructie heeft het kielvlak zijn zijdelingse stabiliteit toch óók eigenlijk alleen van datzelfde stuk hout?

 

[Ariel]

Het zijn niet direct de krachten tijdens het vliegen die het triplex plaatje breken.
Wat een probleem kan worden zijn de klappen tijdens een slechte landing.
Zijn er een aantal houtvezel gebroken moet je niet raar van opkijken dat ineens het kielvlak omklapt tijdens het vliegen.
Ik heb geen ervaring of je zonder kielvlak een toestel aan de grond kunt krijgen zonder verdere schade.

Raymond, volgens mij moet een oplossing zijn om het plaatje te versterken zonder veel extra gewicht.

Johannes

 

[Fotor]

Ik denk ook dat de grote belastingen komen van landingen en misschien de grondrun van een sleepstart. Ik heb wat filmpjes van landingen van mijn vliegtuigen waar de staart extreem heen en weer beweegt (glasvezel rompen) tijdens wat ruwere landingen. Echt veel meer dan je zou denken. Wel een voordeel van deze kist: hij zal niet snel een grondzwaai maken door de combinatie van wielpositie, schaats en zwaartepunt, en als er wel een grondzwaai is zal de staartslof waarschijnlijk boven de grond hangen.

Ik denk dat dit vliegtuig niet te vliegen is als het zijn kielvlak en richtingroer verliest. Er is nogal wat rompoppervlak aanwezig voor het zwaartepunt, hij zou absoluut onstabiel zijn om de topas.

Johannes, heb jij een idee? Ik ben benieuwd. Hieronder nog een afbeelding van hoe het van binnen in elkaar zit (rib 2 is meteen al balsa). Verdikkie, had ik dit maar eerder bedacht, dan had er stevig vliegtuigtriplex gezeten.

 

[DirkSchipper]

Als je de lip die nu uitsteekt afzaagt, en vervolgens in dat kielvlak twee gaten/sleuven freest voor twee gelijksoortige lippen die je tegen de buitenbeplanking (aan de binnenkant) verlijmt, en uiteraard ook kops tegen de balsa 2e rib en aan de onderste populieren rib.
Uiteraard moet er tussen die lip en de buitenbeplanking nog een vulstuk komen om de lippen iets meer naar binnen te zetten, zodat ze in de romp net binnen de gordingen vallen.

Op deze manier heb je die ene centrale lip vervangen door twee uit elkaar staande lippen. Dat is aanzienlijk sterker. Als je die 2 lippen ook nog eens van goede kwaliteit (vliegtuig)triplex maakt, moet het naar mijn gevoel voldoende sterk worden.

Dirk.

 

[jacobbos]

Nog een optie

Een andere versie is 2 nieuwe lippen aanbrengen door het inzagen/infresen van voor en achterlijst. Je kun dan zelfs verder gaan dan de 2e balsa rib, dus door naar de 3e balsa rib.

Ik bedoel dat je dus in het midden van de voor- en achterlijst letterlijk de zaag er in zet met de dikte van het aan te brengen sterke vliegtuig-tri/multiplex. Voordeel is dat de lip ook in de voor en achterlijst houvast heeft. De bestaande lip zaag je gewoon af.

Voordeel is dat je nu niet 1 maar 2 bevestigingspunten hebt, is meteen een stuk sterker.

Even een ruwe schets. Rood zijn de nieuwe lippen

Groet,

Jacob Bos

 

[Fotor]

Ik denk nu aan een iets andere variant. Ik neem jullie suggesties niet 1:1 over, maar jullie hebben mij wel op een goed spoor gezet.

Het uitsteeksel dat er nu zit blijft zitten. Net voor de achterlijst van het kielvlak zaag ik een sleuf uit de wortelrib, idem in de plaat in de romp. Er komt een plaat triplex aan de binnenkant tegen de achterlijst van het kielvlak, dat steekt uit naar beneden en wordt gemonteerd aan het achterste spant van de romp (dus tegen "13" in de foto). In het uitstekende stuk triplex komt nog een sleuf dat om het middenspant van de romp vouwt. Nu heb ik 2 haaks op elkaar staande stukken hout die de krachten opvangen. Het (stevige) stuk hout aan de achterkant vangt de zijdelingse krachten op, het nu bestaande stuk hout neemt de voor/achterwaartse krachten en fixeert de boel verder. Dit 'voelt' in gedachten wel stevig aan.
Dank voor het meedenken!

 

[bdoets]

Okee, ik had over het hoofd gezien de belasting op het kielvlak tijdens starts en landingen.
Maar toch hè... zoals ik al schreef: in de oorspronkelijke constructie zat het kielvlak ook eigenlijk alleen met die centrale lip vast. Misschien zou je de onderste rib dan ook aan de romp vastlijmen, maar dat lijkt me een tamelijk cosmetische verbinding.
Waar het om gaat is: wordt de hele constructie zwakker door die lip vast te schroeven in plaats van te lijmen?
In beide gevallen gaat het om de breuksterkte van de lip. Als-ie gelijmd zit is die breuksterkte niet groter dan als-ie geschroefd zit, toch?

 

[Ariel]

Vier stuks grenenhouten latjes met epoxy vastlijmen.
Eerst gaten boren op de plaats waar de grenen latjes moeten komen en met een vijl de uitsparingen op maat brengen. Gaten moeten ruim om voldoende epoxy tussen triplex en grenen latjes te krijgen.
In het kielvlak bij de tweede rib hoeven geen gaten.
Grenen latjes wel goed tegen de binnenste rib vastlijmen.
De twee berkentriplex plaatjes 1 mm dik moeten ervoor zorgen dat het gaatje niet uitscheurt.

Johannes

 

[Fotor]

Okee, ik had over het hoofd gezien de belasting op het kielvlak tijdens starts en landingen.
Maar toch hè... zoals ik al schreef: in de oorspronkelijke constructie zat het kielvlak ook eigenlijk alleen met die centrale lip vast. Misschien zou je de onderste rib dan ook aan de romp vastlijmen, maar dat lijkt me een tamelijk cosmetische verbinding.
Waar het om gaat is: wordt de hele constructie zwakker door die lip vast te schroeven in plaats van te lijmen?
In beide gevallen gaat het om de breuksterkte van de lip. Als-ie gelijmd zit is die breuksterkte niet groter dan als-ie geschroefd zit, toch?

Bij lijmen zou ik inderdaad de wortelrib van het kielvlak aan de plaat hout op de romp lijmen, dat lijkt me aanzienlijk sterker dan alleen de lip bevestigen (eigenlijk zie ik de functie van die lip niet zo in het normale ontwerp....).

Johannes, ik hoor graag jouw mening op de constructie hierboven die ik zelf bedacht had. Ik denk zelf dat die nog sterker is dan jouw idee.

 

[Ariel]

Het (stevige) stuk hout aan de achterkant vangt de zijdelingse krachten op, het nu bestaande stuk hout neemt de voor/achterwaartse krachten en fixeert de boel verder. Dit 'voelt' in gedachten wel stevig aan.
Dank voor het meedenken!

Zeker de betere oplossing , vooral omdat nu de verbinding kielvlak - romp (krachtinwerking) op de juiste plek zit.

Johannes